1. 가우스 법칙의 응용 : 대칭 전하 분포
전하 분포를 알고 있는 경우 대칭 전하 분포(symmetrical charge distribution)에 대해 가우스 법칙을 이용하여 전속밀도를 계산하는 방법에 대해 알아보자
1) 전하분포를 알고 있는 경우에 대한 가우스 법칙 적용 방법
다음 조건을 만족하는 폐곡면을 선택한다면 쉽게 계산이 가능하다.
(1) 대칭 전하 분포의 가우스 폐곡면 선택 조건
- 가우스 법칙 : \( Q = \oint_s \mathbf{D_s} \bullet d\mathbf{S} \)
- \( \mathbf{D_s} \) 가 모든 점에서 폐곡면 벡터 \( d\mathbf{S} \) 와 평행한 경우 \( (\theta=0) \)
- \( \mathbf{D_s} \bullet d\mathbf{S} = D_sdS \quad (\because \cos\theta = 1) \)
- \( \mathbf{D_s} \) 가 모든 점에서 폐곡면 벡터 \( d\mathbf{S} \) 와 수직인 경우 \( (\theta= \frac{\pi}{2} ) \)
- \( \mathbf{D_s} \bullet d\mathbf{S} = 0 \quad (\because \cos\theta = 0) \)
- 폐곡면 상에서 \( \mathbf{D_s} \) 가 일정한(상수) 경우
- \( Q = \oint_s \mathbf{D_s} \bullet d\mathbf{S} = D_s \oint_s d\mathbf{S} \)
2) 대칭 전하 분포의 가우스 법칙 응용 예시 : 구좌표 원점에 점전하Q가 있는 경우
(1) 가우스 폐곡면 선택 조건
- 그림1과 같이 반경이 r인 구면에 대해 대칭 전하 분포의 폐곡면 선택 조건을 고려하면 다음과 같다.
- \( \mathbf{D_s} \) 방향 : 표면상의 모든 점에서 표면과 수직 즉, \( \mathbf{D_s} // d\mathbf{S} \) 두 벡터가 평행하므로 \( D_s dS \)
- \( \mathbf{D_s} \) 크기 : 폐곡면 상에서 일정 즉, \( Q = D_s\oint_s d\mathbf{S} \)
(2) 가우스 법칙의 정리 과정
- 폐곡면 조건을 고려하여 가우스 법칙을 정리하면 다음과 같다.
- \( Q = \oint_s \mathbf{D_s} \bullet d\mathbf{S} = D_s\oint_s d\mathbf{S} = D_s\oint_s dS \)
- \( dS = r^2\sin\theta d\theta d\phi \)
- 첫번째 적분을 수행하면 다음과 같다.
- \( Q = D_s\oint_s dS = D_s\int_{\phi=0}^{\phi=2\pi}\int_{\theta=0}^{\theta=\pi}r^2\sin\theta d\theta d\phi=D_s r^2\int_{\phi=0}^{\phi=2\pi}\int_{\theta=0}^{\theta=\pi}\sin\theta d\theta d\phi \)
- \( Q = D_s r^2\int_{\phi=0}^{\phi=2\pi}(-\cos\theta|_0^{\pi}) d\phi = 2D_s r^2\int_{\phi=0}^{\phi=2\pi}d\phi \)
- 두번째 적분을 수행하면 다음과 같다.
- \( Q = 2D_s r^2\int_{\phi=0}^{\phi=2\pi}d\phi = 2D_s r^2(\phi|_0^2\pi)=4\pi r^2 D_s \)
- 따라서 정리하면 다음과 같다.
- \( Q = 4\pi r^2 D_s \)
- \( D_s=\frac{Q}{ 4\pi r^2 } \)
- 전속밀도와 전계의 세기의 관계
- \( \mathbf{D}=\frac{Q}{ 4\pi r^2 } \mathbf{a_r} \)
- \( \mathbf{E} =\frac{Q}{ 4\pi \epsilon_0 r^2 } \mathbf{a_r} \)
- \( \mathbf{D} = \epsilon \mathbf{E} \)
3) 대칭 전하 분포의 가우스 법칙 응용 예시 : z축 상에 무한 선전하가 있는 경우

(1) 가우스 폐곡면 선택 조건
- 그림2와 같이 z축 상 \( (-\infty, +\infty) \) 에 대해 선전하 밀도 \( \rho_L \) 이 균일하게 분포되어 있다.
- 선전하의 경우 전속 밀도는 방사상 성분만을 가진다. 따라서 \( \mathbf{D}=D_\rho \mathbf{a_{\rho}} \)
- 폐곡면 구성은 다음과 같다.
- z=0, z=L 사이의 반경이 \( \rho \) 인 원통 표면
- 원통면의 구성 : 상면(top), 하면(bottom), 측면(side)
(2) 가우스 법칙의 정리 과정
- 폐곡면 조건을 고려하여 가우스 법칙을 정리하면 다음과 같다.
- \( Q = \oint_{cyl} \mathbf{D_s} \bullet d\mathbf{S} = \int_{top} \mathbf{D_s} \bullet d\mathbf{S} + \int_{bottom} \mathbf{D_s} \bullet d\mathbf{S} + \int_{side} \mathbf{D_s} \bullet d\mathbf{S} \)
- \( Q = D_s \int_{top} dS + D_s \int_{bottom} dS + D_s \int_{side} dS \)
- 방사상 성분만 존재하므로 \( \rho \) 성분만 고려하여 정리하면 다음과 같다.
- \( Q = 0\int_{top} dS + 0\int_{bottom} dS + D_s\int_{side} dS = D_s\int_{side} dS \)
- \( dS = \rho d\phi dz \)
- \( Q = D_s\int_{side} dS = D_s\int_{z=0}^{z=L}\int_{\phi=0}^{\phi=2\pi}\rho d\phi dz\)
- 첫번째 적분을 수행하면 다음과 같다.
- \( Q = \rho D_s\int_{z=0}^{z=L}(\phi|_0^{2\pi})dz = 2\pi\rho D_s\int_{z=0}^{z=L} dz \)
- 두번째 적분을 수행하면 다음과 같다.
- \( Q = 2\pi\rho D_s\int_{z=0}^{z=L} dz = 2\pi\rho(z|_0^L)= 2\pi\rho LD_s\)
- 따라서 가우스 법칙을 정리하면 다음과 같다.
- \( Q = 2\pi\rho LD_s \)
- \( D_s=D_\rho=\frac{Q}{ 2\pi\rho L } = \frac{\rho_L}{ 2\pi\rho} \quad (\because Q=\rho_L L) \)
- 전속밀도와 전계의 세기의 관계
- \( D= \frac{\rho_L}{ 2\pi\rho} \)
- \( E = \frac{\rho_L}{ 2\pi\epsilon_0\rho} \)
- \( \mathbf{D} = \epsilon \mathbf{E} \)
4) 대칭 전하 분포의 가우스 법칙 응용 예시 : 동축 케이블(coaxial cable)의 경우

(1) 가우스 폐곡면 선택 조건
- 그림3과 같이 내경이 a, 외경이 b, 길이가 무한인 두개의 동축 원통 도체가 있다.
- 전하 : 내부 및 외부 도체의 표면에 존재한다 즉, 표면전하 밀도 \( \rho_s \) 로 존재
- 대칭성을 고려하면 원통 좌표계로 표현할 수 있다.
- \( \mathbf{D_s} = D_\rho \mathbf{a_\rho}+ D_\phi \mathbf{a_\phi }+ D_z \mathbf{a_z} \)
- 폐곡면 구성은 다음과 같다.
- \( \rho = [a,b], < a, > b , \quad \phi = [0, 2\pi] , \quad z = [0,L] \)
(2) 가우스 법칙의 정리 과정 : \( a < \rho < b \)

- 폐곡면 : 길이 L, 반경 \( \rho \) 인 직선형 원통(= 3) 선전하와 동일)
- 내부 도체구의 표면 전하 밀도만 고려되므로 반경은 다음과 같다.
- \( \rho=a \)
- 직선형 원통 폐곡면을 봤을 때 3) 선전하와 동일하게 표현된다.
- \( Q = D_s 2\pi \rho L\)
- 전하Q에 대해 표면전하 밀도로 표현하면 다음과 같다.
- \( Q = \int \rho_s dS \)
- \( dS = \rho d\phi dz = ad\phi dz \)
- \( Q = \int_{z=0}^{z=L} \int_{\phi=0}^{\phi=2\pi} \rho_s ad\phi dz=2\pi aL\rho_s \)
- \( \int dS \) 에 대해 다른 방법으로 접근해보자
- 총 면적 S : 내부 도체의 표면과 같으므로 다음과 같이 생각해보자.
- 내부 도체를 z축 방향으로 잘라서 핀다고 생각하면 사각형을 생각할 수 있다.
- z축 방향 = 세로 길이 = \( \mathbf{L} = L\mathbf{a_z} \)
- 원주 길이(= 각도 방향) = 가로 길이 = \( 2\pi r = 2\pi\rho = 2\pi a\mathbf{a_\phi} \)
- 표면 전하 밀도 적분 결과와 동일한 것을 다음과 같이 알 수 있다.
- \( \rho_s\int dS = 2\pi aL\rho_s \)
- 따라서 전하 Q에 대해 다음과 같이 표현할 수 있다.
- \( Q = D_s 2\pi \rho L = 2\pi aL\rho_s \)
- \( D_s = \frac{a\rho_s}{\rho} \to \mathbf{D_s} = \frac{a\rho_s}{\rho}\mathbf{a_r} \)
- \( Q = 2\pi aL\rho_s = \rho_L L \to \rho_L = 2\pi a\rho_s \to \rho_s=\frac{\rho_L}{2\pi a} \)
- \( \rho_s \) 에 \( \rho_L \) 식을 대입하면 무한 선전하의 전속 밀도 식과 동일함을 알 수 있다.
(3) 가우스 법칙의 정리 과정 : \( \rho < a \)
- 해당 반경을 가우스 폐곡면으로 사용하는 경우 다음과 같이 표현된다.
- 표면 전하 내부가 폐곡면인 상황
- 전하로부터 전속이 발생되기 때문에 발생되는 전속이 없는 상황
- 따라서, 폐곡면을 통과하는 전속이 없다.
- 도체 내부에 전하량이 없다.
(4) 가우스 법칙의 정리 과정 : \( \rho > b \)
- 해당 반경을 가우스 폐곡면으로 사용하는 경우 다음과 같이 표현된다.
- 반경 a인 내부 도체의 표면전하에 양전하(+Q)가 있다면 반경 b인 외부 도체의 표면전하에 유도전하(-Q)가 존재하게 된다.
- 따라서 두 표면 전하에 의해 전계와 전속이 모두 상쇄되므로 폐곡면을 통과하는 전속이 없다.
(5) 동축 케이블(동축 커페시터)의 특징
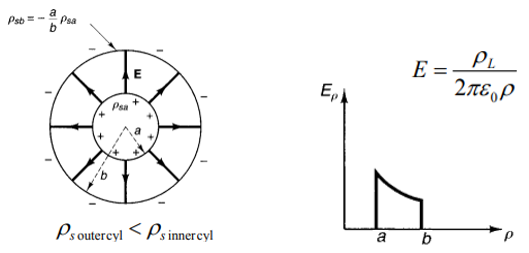
- 동축 케이블의 내부 및 외부 표면 전하 밀도는 다음과 같다.
- \( Q_{inner cyl} = 2\pi aL \rho_{s, inner cyl} \)
- \( Q_{outer cyl} = -2\pi bL \rho_{s, outer cyl} \)
- \( Q_{outer cyl} = -\frac{a}{b}L \rho_{s, inner cyl} \)
- 동축 케이블 또는 동축 커페시터의 특징
- 외부에 전계를 갖지 않는다. 즉, 외부 도체가 차폐(Shield) 역할을 한다.
- 중심 도체(내부 도체) 내부에에 전하량이 없다.
'Engineering Electromagnetism > 3. Electric Flux&Gauss's Law&Divergence' 카테고리의 다른 글
| Chapter 3-5 발산과 맥스웰의 첫 번째 방정식 (1) | 2025.03.05 |
|---|---|
| Chapter 3-4 가우스 법칙의 응용 : 미소체적소 (1) | 2025.03.05 |
| Chapter 3-2 가우스 법칙(Gauss's Law) (0) | 2025.03.04 |
| Chapter 3-1 전속 밀도(Electric Flux Density) (1) | 2025.03.04 |




