1. 전계 내에서 점전하를 이동시키는데 소요되는 에너지
Chapter 3에서 전속 밀도와 가우스 법칙을 통해 멕스웰의 첫번째 방정식을 도출했다면
Chapter 4장에서는 전계에서의 에너지 개념과 전위(Potential)를 도입하여 전계에 대해 새로운 관점에서 바라보고 이해할 예정이다.
즉, Chapter 4는 전계에 대해 에너지와 전위의 관점에서 다루고 배우며, 이를 통해 전계의 물리적 의미를 더욱 심화하는 과정이다.
1) 전계 내에서 점전하의 이동

(1) 전계 내 점전하의 이동과 일의 관계
- 전계의 세기(Electric Field Intensity) : 공간 내의 한 전하에 의해 단위 시험 전하(+1C)가 받는 힘
- 그림 1과 같이 단위 시험 전하를 전계와 반대 방향으로 이동하는 경우 다음과 같다.
- 전계에 의한 힘의 크기는 같고 반대 방향인 힘이 필요
- 즉, 외부에서 일을 해야 한다 = 에너지를 소비해야 한다 = 양의 에너지가 필요
- 단위 시험 전하를 전계와 같은 방향으로 이동하는 경우 다음과 같다.
- 외부에서 가해줘야 할 에너지는 음의 에너지
- 즉, 전계가 일을 한다.
(2) 전계 \( \mathbf{E} \) 내에서 전하 \( Q \) 를 거리 \( d\mathbf{L} \) 만큼 이동시키는 경우
- 전계에 의해 Q에 작용하는 힘은 다음과 같다.
- \( \mathbf{F}_E = Q\mathbf{E} \)
- 힘의 \( d\mathbf{L} \) 방향의 성분 \( \mathbf{F}_{EL} \) 은 다음과 같다.
- \( F_{EL} = \mathbf{F}_E \bullet \mathbf{a}_L = Q\mathbf{E} \bullet \mathbf{a}_L \)
- 전하를 이동시키기 위해 외부에서 전하에 가해야 할 힘은 다음과 같다.
- 전계에 의한 힘의 크기는 같고, 방향은 반대이어야 한다.
- \( F_{appl} = - Q\mathbf{E} \bullet \mathbf{a}_L \)
- 전하를 \( d\mathbf{L} \) 만큼 이동시키는 데 필요한 에너지(소요된 일)
- \( W = FL \) : 에너지는 힘과 거리의 곱
- \( dW = F_{appl} dL = - Q\mathbf{E} \bullet \mathbf{a}_L dL = - Q\mathbf{E} \bullet d\mathbf{L} \)
- 미소 일(\( dW \)) 가 0이 되는 조건
- \( \mathbf{E} \) , \( Q \) , \( d\mathbf{L} \) 중 하나가 0이 되는 경우 - 무의미
- \( \mathbf{E} \) , \( d\mathbf{L} \) 가 직각이 되는 경우 : \( \cos\theta=0 \)
- 따라서 전계 내에서 전하를 유한 거리만큼 이동시키는데 필요한 일은 다음과 같다.
- \( W = -Q\int_{init}^{final} \mathbf{E} \bullet d\mathbf{L} \)
- 즉, 선적분(Line integral)으로 표현된다.
2) 선적분(Line Integral)

(1) 선적분의 적분 경로
- 전계 내에서 전하를 유한 거리만큼 이동시키는데 필요한 일은 위와 같이 선적분으로 표현된다.
- \( W = -Q\int_{init}^{final} \mathbf{E} \bullet d\mathbf{L} \)
- 그림2와 같이 균일한 전계 내에 대한 적분 경로는 시작점 B(initial point) 에서 종점 A(final point) 까지 선적분을 생각해보자.
- 6개로 경로를 분리하여 각 선분의 구성 : \( \Delta L_1, \Delta L_1, ..., \Delta L_6 \)
- 각 선분 벡터 방향의 전계의 세기 성분 : \( E_{L1}, E_{L2}, ..., E_{L6} \)
- 적분 경로로 전하 Q를 이동시키는데 필요한 일의 근사치는 다음과 같다.
- \( W = -Q(E_{L1}\Delta L_1+ E_{L2}\Delta L_2 +...+ E_{L6}\Delta L_6) \)
- \( W = -Q(\mathbf{E}_{1}\bullet\Delta \mathbf{L}_1+ \mathbf{E}_{2}\bullet\Delta \mathbf{L}_2 +...+ \mathbf{E}_{6}\bullet\Delta \mathbf{L}_6 ) \)
- 전계가 균일하다고 가정되어 있으므로 다음과 같다
- \( \mathbf{E1} = \mathbf{E1} = ... = \mathbf{E6} \)
- 따라서 다음과 같이 표현된다.
- \( W = -Q\mathbf{E}\bullet(\Delta L_1+ \Delta L_2 +...+ \Delta L_6) \)
- 괄호 안의 선분벡터의 합은 전체 선분 벡터 \( \mathbf{L}_{BA} \) 와 동일 하므로 다음과 같다.
- \( W = -Q\mathbf{E}\bullet\mathbf{L_{BA}} \) (E : 균일)
- 즉, 정분 경로와 무관하다는 것을 알 수 있다
(2) 선적분을 통한 전하를 이동시키는데 필요한 일
- 일은 선적분으로 정의되고, 전계가 균일한 경우(상수) 다음과 같이 표현된다.
- \( W = -Q \mathbf{E} \bullet \int_{B}^{A} d\mathbf{L} = -Q \mathbf{E} \bullet \mathbf{L}_{BA} \)
- 전하를 이동시키는데 필요한 일의 결정 요소는 다음과 같다.
- \( \mathbf{E} \) , \( Q \) , \( \mathbf{L}_{BA} \)
- 단. 전계는 균일하다는 가정이 존재한다.
- 좌표계에 따른 거리 \( d\mathbf{L} \) 는 다음과 같이 정리된다.
- \( d\mathbf{L} = dx \mathbf{a_x} + dy \mathbf{a_y} + dz \mathbf{a_z} \quad \text{(rectangular)} \)
- \( d\mathbf{L} = d\rho \mathbf{a_{\rho}} + \rho d\phi \mathbf{a_{\phi}} + dz \mathbf{a_z} \quad \text{(cylindrical)} \)
- \( d\mathbf{L} = dr \mathbf{a_r} + r d\theta \mathbf{a_{\theta}} + r \sin\theta d\phi \mathbf{a_{\phi}} \quad \text {(spherical)} \)
(3) 무한 선전하에 의한 전계 내 여러 적분로에 관한 고찰 : 원주 방향(원 둘레 일주)인 경우
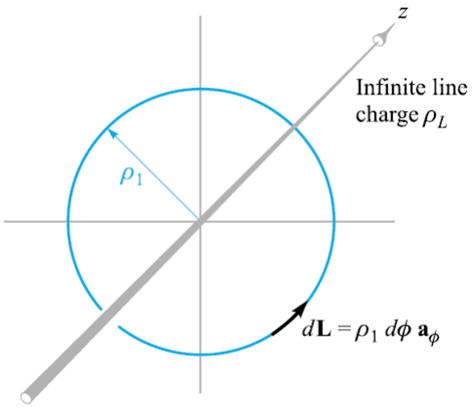
- 그림3과 같이 양전하 Q가 반경 \( \rho_1 \)인 원 둘레를 일주하는 데 필요한 일에 대해 알아보자
- 이동 경로는 항상 전계 방향과 수직이므로 소요되는 일은 0이 될 것이다.
- 일에 대한 정의는 다음과 같다.
- \( W = -Q\int_{B}^{A} \mathbf{E} \bullet d\mathbf{L} \)
- 일을 계산하는데 필요한 선전하 밀도에 의한 전계의 세기는 다음과 같다.
- \( \mathbf{E} = E_\rho\mathbf{a_\rho}=\frac{\rho_L}{2\pi\epsilon\rho}\mathbf{a_\rho} \)
- 일을 계산하는데 필요한 거리는 원통 좌표계의 거리를 사용 하면 다음과 같다
- \(d\mathbf{L} = \rho d\phi\mathbf{a_{\phi}} \quad (\because d\rho\mathbf{a_\rho}=dz\mathbf{a_z}=0) \)
- 원주를 일주하기 때문에 \( \rho , z \) 방향으로의 경로 성분이 0이 됨을 알 수 있다.
- 일을 구하는 식에 대입하면 다음과 같다.
- \( W = -Q \int_{B}^{A} \frac{\rho_L}{2\pi\epsilon_0\rho_1} \mathbf{a_\rho} \cdot \rho_1 d\phi \mathbf{a_{\phi}} = -Q \int_{0}^{2\pi} \frac{\rho_L}{2\pi\epsilon_0} d\phi \mathbf{a_\rho} \cdot \mathbf{a_{\phi}} = 0 \)
(4) 무한 선전하에 의한 전계 내 여러 적분로에 관한 고찰 : 방사상 방향인 경우

- 그림 4와 전하를 \( \rho=a\to b\) 로 이동시키는데 필요한 일에 대해 알아보자.
- 일에 대한 정의와 일을 계산하는데 필요한 선전하 밀도는 그림3의 예시와 동일하다.
- 일을 계산하는데 필요한 거리는 원통 좌표계의 거리를 사용 하면 다음과 같다
- \(d\mathbf{L} = d\rho\mathbf{a_{\rho}} \quad (\because \rho d\phi\mathbf{a_\phi}=dz\mathbf{a_z}=0) \)
- 방사상 방향이므로 \( \phi , z \) 방향으로의 경로 성분이 0이 됨을 알 수 있다.
- 일을 구하는 식에 대입하면 다음과 같다.
- \( W = -Q \int_{\text{init}}^{\text{final}} \frac{\rho_L}{2\pi\epsilon_0\rho} \mathbf{a_\rho} \cdot d\rho \mathbf{a_\rho} = -Q \int_{a}^{b} \frac{\rho_L}{2\pi\epsilon_0} \frac{d\rho}{\rho} = -Q \frac{\rho_L}{2\pi\epsilon_0} \ln\rho \Big|_{a}^{b} = -\frac{Q \rho_L}{2\pi\epsilon_0} \ln\frac{b}{a} \)
- \( b>a \to \ln\frac{b}{a} >0 \to W < 0 \)
- 외부에서 가해줘야 할 에너지가 음의 에너지라는 것은 전계가 일은 한다는 것이다.
- 전계가 일을 한다는 것은 에너지를 받는다는 의미이다.
- 이번에는 반대로, 전하를 \( \rho=a\to b\) 로 이동시키는데 필요한 일에 대해 알아보자.
- \( W = -Q \int_{b}^{a} \frac{\rho_L}{2\pi\epsilon_0} \frac{d\rho}{\rho} = -Q \frac{\rho_L}{2\pi\epsilon_0} \ln\rho \Big|_{b}^{a} = \frac{Q \rho_L}{2\pi\epsilon_0} \ln\frac{b}{a} \)
- 에너지의 부호가 +로 바뀐 것으로 보아 외부에서 일을 해주어야 한다는 것이다.
- 즉, 에너지를 소모한다.
'Engineering Electromagnetism > 4. Electric Field Energy&Potential' 카테고리의 다른 글
| Chapter 4-6 정전계 내의 에너지 밀도(Energy Density in the Electrostatic Field) (0) | 2025.03.17 |
|---|---|
| Chapter 4-5 전기 쌍극자(The Electric Dipole) (0) | 2025.03.12 |
| Chapter 4-4 전위 경도(Potential Gradient) (0) | 2025.03.10 |
| Chapter 4-3 전하계에 의한 전위 : 보존적 성질 (0) | 2025.03.10 |
| Chapter 4-2 전위차와 전위의 정의 (0) | 2025.03.07 |



