1. 전위차와 전위의 정의
전계에서의 새로운 물리량인 전위(Potential)에 대해 알아보자.
1) 전위차 및 전위의 정의(Definition of Potential Difference and Potential)

(1) 전위차(Potential Difference)
- 정의
- 그림 1과 같이 한 전하에 의한 전계 내에서 단위 양 전하(+!C)를 한 점에서 다른 한 점까지 이동시키는데 외부에서 가해 주어야 할 일
- \( V = \frac{W}{Q} = -\int_{init}^{final} \mathbf{E} \bullet d\mathbf{L} \)
- 따라서, 전위차와 전위는 Scalar Field 이다.
- 단위 : \( (J/C) , V \)
- 표시 : \( V_{AB} \)
- 단위 양전하를 점 B에서 A까지 이동시키는 데 필요한 일
- 선적분으로 시점이 B, 종점이 A를 의미
- 전위차 \( V_{AB} \) 의 부호
- 양전하를 B에서 A까지 이동시키는데 외부에서 일을 해주어야 하는 경우 양의 부호
- 선전하에서의 \( V_{AB} \)
- \( \rho =a, \rho =b \) 점 사이 전위차는 다음과 같다.
- \( V_{ab} = \frac{W}{Q} = \frac{\rho_L}{2\pi\epsilon_0} \ln{\frac{b}{a}} \)
- 선전하에서의 전위차에서 W에 대한 식이 궁금하다면 이전 포스팅 참고
- 일과 전위차의 관계는 다음과 같다.
- \( W=QV \to V=\frac{W}{Q} \)
(2) 전위(Potential)
- 정의 :
- 절대 전위
- 편의상 어느 특정 기준점의 전위를 0으로 하고, 이 점과 어느 한 점과의 전위차를 표시할 때에 한해서 사용
- 전위차 대신 전위(Potential)이라 한다.
- 보편적인 0 전위 기준점 : 대지면(ground, 무한 평면=지구 표면)
- 또 다른 0 전위 기준점 : 무한원점(지구표면에 떨어진 곳에서의 전위를 논하는 경우)
- 예시
- 점 A의 전위를 \( V_A \) 점 B에의 전위를 \( V_B \)라 하면 \( V_{AB}=V_A-V_B \) 이다
- 단. 두 전위는 동일한 0 전위기준점을 가진다.
(3) 등전위면
- 정의 : 같은 정위 값을 가지는 모든 점들로 이루어진 표면
- 특성 : 등전위면상에 임의의 두 점 사이 전위차는 0
- 즉, 등전위면상에서 단위 전하를 이동시키는데 필요한 일은 없다.
2) 전하에 의한 전위차와 전위(Potential Field of a Charge )
(1) 전하에 의한 전위와 전위차
- 전위차의 정의에 의해 다음과 같이 표현된다.
- \( V = \frac{W}{Q} = -\int_{init}^{final} \mathbf{E} \bullet d\mathbf{L} \)
- 즉, 전위차와 전위는 전하에 의한 전계의 세기와 좌표계에 의한 거리 따라 결정된다.
- 전하에 의한 전계의 세기 \( \mathbf{E} \) 정리
- \( \text{Point Charge : } \mathbf{E} = \frac{Q}{4\pi\epsilon_0 r^2}\mathbf{a}_r \)
- \( \text{Line Charge : } \mathbf{E} = \frac{\rho_L}{2\pi\epsilon_0\rho}\mathbf{a}_\rho \)
- \( \text{Sheet of Charge : } \mathbf{E} = \frac{\rho_s}{2\epsilon_0}\mathbf{a}_N \)
- 좌표계에 따른 거리 \( d\mathbf{L} \) 는 정리
- \( d\mathbf{L} = dx \mathbf{a_x} + dy \mathbf{a_y} + dz \mathbf{a_z} \quad \text{(rectangular)} \)
- \( d\mathbf{L} = d\rho \mathbf{a_{\rho}} + \rho d\phi \mathbf{a_{\phi}} + dz \mathbf{a_z} \quad \text{(cylindrical)} \)
- \( d\mathbf{L} = dr \mathbf{a_r} + r d\theta \mathbf{a_{\theta}} + r \sin\theta d\phi \mathbf{a_{\phi}} \quad \text {(spherical)} \)
(2) 점전하에 의한 전위와 전위차
- 점전하에 의한 전계의 세기와 이를 고려한 미소 거리는 다음과 같다.
- \( \mathbf{E} = \frac{Q}{4\pi\epsilon_0 r^2}\mathbf{a}_r \)
- \( d\mathbf{L} = dr \mathbf{a_r} + r d\theta \mathbf{a_{\theta}} + r \sin\theta d\phi \mathbf{a_{\phi}} \)
- \( d\mathbf{L} = dr \mathbf{a_r} \quad (\because r d\theta \mathbf{a_{\theta}} = r \sin\theta d\phi \mathbf{a_{\phi}} =0) \)
- 전위차 식에 대입하면 다음과 같다.
- \( V = -\int_{B}^{A} \frac{Q}{4\pi\epsilon_0 r^2}\mathbf{a}_r \bullet dr \mathbf{a_r}= -\frac{Q}{4\pi\epsilon_0}\int_{B}^{A}\frac{dr}{r^2}= -\frac{Q}{4\pi\epsilon_0}(-\frac{1}{r}\Big|_B^A)=\frac{Q}{4\pi\epsilon_0}(\frac{1}{r_A}-\frac{1}{r_B}) \)
- 따라서 다음과 같은 결론을 얻는다.
- 거리 B가 A보다 크다면 전위차의 부호 양수이므로 외부에서 에너지를 소모하게 된다.
- \( r_B>r_a \to V_{AB}>0 \)
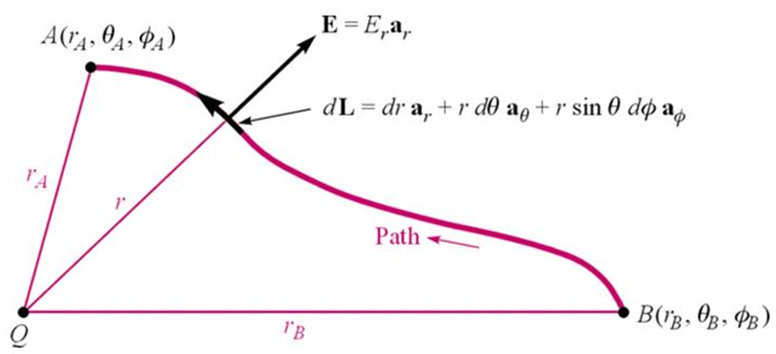
- 그림2와 같이 두 점 사이의 이동경로가 복잡한 경우에 대해 생각해보자.
- 미소 선분 벡터는 다음과 같다.
- \( d\mathbf{L} = dr \mathbf{a_r} + r d\theta \mathbf{a_{\theta}} + r \sin\theta d\phi \mathbf{a_{\phi}} \)
- 위와 마찬가지로 전계의 세기는 \( \mathbf{a}_r \) 성분만 가지므로 나머지 성분이 0이 된다
- 이동경로가 복잡한 경우에도 위와 같은 결론을 얻을 수 있다.
- 즉, 두 점 사이의 원점으로부터 거리에 의해 결정되며, 이동 경로와는 무관하다.
- 전위에 대한 식은 무한 원점을 0으로 하는 경우이므로 다음과 같다.
- \( V = \frac{1}{4\pi\epsilon_0}\frac{Q}{r} \)
- 전계 내 단위 전하를 무한 원점으로부터 전하 Q에서 r만큼 떨어진 점까지 이동시키는데 외부에서 가해주어야 할 일을 의미한다
- 특정 0 기준점을 선택하지 않고 전위를 표현하는 방법
- \( r_A \to r \) 로 표현하고 \( \frac{Q}{4\pi\epsilon_0 r_B} \) 에 대해 상수로 두는 것이다.
- \( V =\frac{Q}{4\pi\epsilon_0}(\frac{1}{r_A}-\frac{1}{r_B}) = \frac{Q}{4\pi\epsilon_0 r_A}- \frac{Q}{4\pi\epsilon_0 r_B} = \frac{1}{4\pi\epsilon_0}\frac{Q}{r} + C_1 \)
- 여기서 \( C_1 \)은 임의의 r값에서 V가 임의의 값을 갖도록 전위 기준점을 정하는 것이다.
- 즉, \( r=r_0 \) 에서 \( V=V_0 \) 가 되도록 전위 기준점을 정하는 것이다
- \( V_0 = \frac{1}{4\pi\epsilon_0}\frac{Q}{r_0} + C_1 \to V = \frac{1}{4\pi\epsilon_0}\frac{Q}{r} + V_0 -\frac{1}{4\pi\epsilon_0}\frac{Q}{r_0} \)
(3) 선전하에 의한 전위차
- 선전하에 의한 전계의 세기와 이를 고려한 미소 거리는 다음과 같다.
- \( \mathbf{E} = \frac{\rho_L}{2\pi\epsilon_0\rho}\mathbf{a}_\rho \)
- \( d\mathbf{L} = d\mathbf{L} = d\rho \mathbf{a_{\rho}} + \rho d\phi \mathbf{a_{\phi}} + dz \mathbf{a_z} \)
- \( d\mathbf{L} = d\rho \mathbf{a_{\rho}} \quad (\because \rho d\phi \mathbf{a_{\phi}} = dz \mathbf{a_z} =0) \)
- 전위차 식에 대입하면 다음과 같다.
- \( V = -\int_{B}^{A} \frac{\rho_L}{2\pi\epsilon_0\rho}\mathbf{a}_\rho \bullet d\rho \mathbf{a_{\rho}} = -\frac{\rho_L}{2\pi\epsilon_0}\int_{B}^{A}\frac{d\rho }{\rho}= -\frac{\rho_L}{2\pi\epsilon_0}(\ln\rho\Big|_B^A)=\frac{\rho_L}{2\pi\epsilon_0}\ln{\frac{B}{A}} \)
'Engineering Electromagnetism > 4. Electric Field Energy&Potential' 카테고리의 다른 글
| Chapter 4-6 정전계 내의 에너지 밀도(Energy Density in the Electrostatic Field) (0) | 2025.03.17 |
|---|---|
| Chapter 4-5 전기 쌍극자(The Electric Dipole) (0) | 2025.03.12 |
| Chapter 4-4 전위 경도(Potential Gradient) (0) | 2025.03.10 |
| Chapter 4-3 전하계에 의한 전위 : 보존적 성질 (0) | 2025.03.10 |
| Chapter 4-1 전계 내에서 점전하를 이동시키는데 소요되는 에너지 (0) | 2025.03.06 |



