1. 전기 쌍극자(Electric Dipole)
이번 Chapter에서 새로운 개념인 전기 쌍극자에 대해서 알아보자.
쌍극자(Eiople)는 Chaper 6의 전계 내 유전체 물질의 거동에 대한 기초를 다룬다. 뿐만 아니라 Chapter 5의 영상(image) 기법에 대한 기초도 다루기 때문에 미리 잘 이해해두면 도움이 될 것이다.
이번 Chapter의 전개 과정은 전위계와 전계의 관계 대한 개념을 이해하는데에도 도움이 될 것이다.
1) 전기 쌍극자(Electric Dipole)
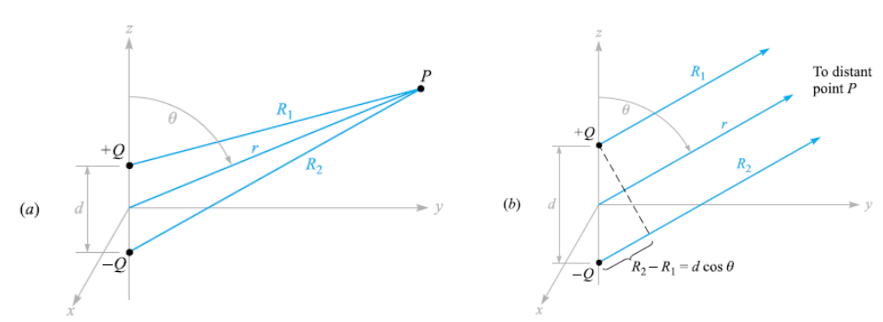
(1) 전기 쌍극자의 정의
- 크기가 같고 부호가 반대인 두 점전하 \( (+Q, -Q) \) 가 매우 가까운 거리 d만큼 떨어져 있는 전하의 배열
- 두 전하의 간격과 점P와의 거리는 다음과 같은 가정을 만족한다.
- \( r >> d \)
- 그림 1과 같이 양전하(+Q)와 음전하(-Q)는 거리 d만큼 떨어져 원점으로부터 동일한 거리에 위치하므로 다음과 같이 표현된다.
- \( +Q(0,0,\frac{1}{2}d) \)
- \( -Q(0,0,-\frac{1}{2}d) \)
- 먼 거리인 점P는 구좌표계를 사용하여 다음과 같이 표현된다.
- \( P(r,\theta,\phi=\frac{\pi}{2}) \)
- 쌍극자는 z축 상에 존재하므로 점P에 대해 방위각 대칭이다.
- 쌍극자가 z축 상에 존재하므로 전계와 전위계 내 점P에 대해 \( \phi \) 가 변하지 않는단는 의미
- 전계 \( \mathbf{E} \) 와 전위 \( V \) 중 더 계산이 간단한 물리량을 우선으로 구하는 것이 계산상 편하다
- 전계의 세기 먼저 구하는 방법
- 구좌표계의 두 성분 구해야 한다
- 대칭성에 의해 \( E_\phi=0 \) 이므로 \( E_\rho, E_\theta \) 만 고려하면 된다.
- 단, 전위를 구할 때 선적분을 수행해야 하며, 적절한 기준 전위를 설정해야 한다.
- 전위 먼저 구하는 방법
- 각 점전하에 대한 전위의 합으로 간단하게 계산 가능하다.
- 전계의 세기는 \( \text{grad V} \) 로 계산 가능하다.
(2) 전기 쌍극자에 대한 전위
- 그림 1의 (a)와 같이 점전하 Q, -Q에서 점 P에 대한 전위는 다음과 같이 표현된다.
- \( V = \frac{Q}{4\pi\epsilon_0} (\frac{1}{R_1}- \frac{1}{R_2}) = \frac{Q}{4\pi\epsilon_0}\frac{R_2-R_1}{R_1 R_2 } \)
- \( +Q \) 에서 점 P까지의 거리 : \( R_1 \)
- \( -Q \) 에서 점 P까지의 거리 : \( R_2 \)
- 원점에서 점P 까지의 거리 : \( r \)
- \(R_1 = R_2 \) : z=0인 평면은 두 점전하의 중간이므로 거리가 같으므로 전위는 0이 된다
- 그림 1의 (b)와 같이 점 P가 매우 먼 거리에 있다고 가정해보자
- 점 P가 매우 먼 거리로 멀어지면서 각 지점에서의 거리 \( R_1, R_2, r \) 가 모두 평행하다고 볼 수 있다.
- 두 전하로부터 점 P까지의 거리를 모두 \( r \)로 표현하면 다음과 같다.
- \( R_1, R_2 \approx r \to R_1R_2 =r^2 \)
- \( R_1 = r - \frac{d}{2}\cos\theta \) : \( r \) 로 표현하기 위해 \( R_1 \to r \) 로 투영 후 길이 반영(r보다 작음 - )
- \( R_2 = r + \frac{d}{2} \cos\theta \) : \( r \) 로 표현하기 위해 \( R_2 \to r \) 로 투영 후 길이 반영(r보다 큼 + )
- \( R_2-R_1 = d\cos\theta \)
- 그림 1의 (b)와 같이 점 P거리가 매우 먼 경우에 대한 전위는 다음과같다.
- \( V= \frac{Q}{4\pi\epsilon_0}\frac{R_2-R_1}{R_1 R_2 } = \frac{Q}{4\pi\epsilon_0} \frac{d\cos\theta}{r^2} \quad (\because R_1R_2=r^2, R_2-R_1=d\cos\theta) \)
- \( z=0 \to \theta = \frac{\pi}{2} \to cos\theta = 0 \)
- 그림 1의 (a)와 같이 두 점전하의 중간인 z=0일 때 전위가 0임을 알 수 있다.
(3) 전기 쌍극자에 대한 전계의 세기
- 전위를 이용한 전계의 세기는 다음과 같은 식을 이용할 수 있다.
- \( \mathbf{E} = - \text{grad V} = -\nabla V = \frac{\partial V}{\partial r} \mathbf{a_r} + \frac{1}{r} \frac{\partial V}{\partial \theta} \mathbf{a_{\theta}} + \frac{1}{r \sin \theta} \frac{\partial V}{\partial \phi} \mathbf{a_{\phi}} \quad \text{(Spherical)} \)
- 위에서 구한 전위를 대입하면 다음과 같다.
- \( \mathbf{E} = -\nabla V = -\nabla \frac{Qd}{4\pi\epsilon_0} \frac{d\cos\theta}{r^2} \)
- \( \frac{\partial V}{\partial r} \mathbf{a_r} = \frac{Qd}{4\pi\epsilon_0}(-2\frac{d\cos\theta}{r^3})= -\frac{Qd}{2\pi\epsilon_0}(\frac{d\cos\theta}{r^3}) \)
- \( \frac{1}{r} \frac{\partial V}{\partial \theta} \mathbf{a_{\theta}} = \frac{Qd}{4\pi\epsilon_0 r}(-\frac{d\sin\theta}{r^2}) = -\frac{Qd}{4\pi\epsilon_0}(\frac{d\sin\theta}{r^3}) \)
- 따라서 정리하면 다음과 같다.
- \( \mathbf{E} = -\nabla V = -(-\frac{Qd}{2\pi\epsilon_0}(\frac{d\cos\theta}{r^3})-\frac{Qd}{4\pi\epsilon_0}(\frac{d\sin\theta}{r^3}))=\frac{Qd}{4\pi\epsilon_0 r^3}(2\cos\theta\mathbf{a}_r+\sin\theta\mathbf{a}_\theta) \)
(4) 쌍극자에 의한 전계와 전위
- 전위는 거리의 제곱에 반비례 한다.
- \( V \propto \frac{1}{r^2} \)
- 전계의 세기는 거리의 세제곱에 반비례 한다.
- \( E \propto \frac{1}{r^3} \)
- 쌍극자에 의한 전계와 전위가 단일 점전하의 경우보다 더 빠르게 감소한다.
- 서로 반대 부호를 가진 전하들이 거리가 멀 수록 더 가까워 보이게 되고, 하나의 점(총 전하량이 0)인 것처럼 작용한다.
- 쯕, 쌍극자는 먼 거리에서 전계가 약해진다.
2) 등전위계(Equipotential Field)와 전계의 유선(Streamlines)

(1) 등전위계 그래프
- 전기 쌍극자에 의한 전위식은 다음과 같다.
- \( V=\frac{Qd}{4\pi\epsilon_0} \frac{d\cos\theta}{r^2} \)
- 전위계의 그림을 얻기 위해 다음과 같이 설정할 수 있다.
- \( \frac{Qd}{4\pi\epsilon_0} =1 \to V_0 = \frac{\cos\theta}{r^2} \)
- \( r = \sqrt{\frac{1}{V_0}\cos\theta} \)
- 따라서 그림 2의 파란선(blue line)과 같이 등전위선이 나타난다.
- \( V = 0, +0.2, +0.4 +0.6, +0.8, +1.0 \)
- 전기 쌍극자는 세로 축인 z축 상에 있고, 위쪽에 양전하(+Q) 아래쪽에 음전하(-Q)가 있다
(2) 전계의 유선 그래프
- 전계의 유선은 전기력선으로 전계의의 방향을 따라 그려진 곡선(경로)은 다음과 같은 특징을 갖는다.
- 전계의 유선은 등전위면과 항상 직각을 이룬다.
- 유선은 전계의 방향 벡터와 접선을 이룬다.
- 유선의 임의의 한 점에 대한 접선 벡터는 그 점에서의 전계와 같은 방향(평행) 이다.
- 전기 쌍극자에 의한 전계의 세기는 다음과 같다.
- \( \mathbf{E} =E_r\mathbf{a}_r+ E_\theta\mathbf{a}_\theta \)
- \( \mathbf{E} = \frac{Qd}{4\pi\epsilon_0 r^3}(2\cos\theta\mathbf{a}_r+\sin\theta\mathbf{a}_\theta) \)
- 전계와 같은 방향(평행)인 유선의 임의의 한 점에 대한 미소 변위 벡터는 다음과 같다.
- \( d\mathbf{L} = dr\mathbf{a}_r+ rd\theta\mathbf{a}_\theta + r\sin\theta d\phi\mathbf{a}_\phi \)
- \( d\mathbf{L} = dr\mathbf{a}_r+ rd\theta\mathbf{a}_\theta \quad (\because \mathbf{a}_\phi = 0 ) \)
- 두 벡터의 평행 조건
- 두 벡터가 평행하다는 의미는 한 벡터가 다른 벡터의 스칼라배로 표현된다는 것이다.
- \( \mathbf{E} = k d\mathbf{L} \)
- \( E_r\mathbf{a}_r+ E_\theta\mathbf{a}_\theta = k( dr\mathbf{a}_r+ rd\theta\mathbf{a}_\theta ) \)
- k에 대해서 모든 성분이 동일한 비율로 증가해야 하므로 다음과 같이 표현된다.
- \( k = \frac{E_r}{dr} = \frac{E_\theta}{rd\theta} \)
- \( \frac{E_\theta}{E_r} = \frac{rd\theta}{dr} \)
- 위 관계를 이용하여 정리하면 다음과 같다.
- \( \frac{E_\theta}{E_r} = \frac{rd\theta}{dr} =\frac{\sin\theta}{2\cos\theta} \)
- \( \frac{rd\theta}{dr} =\frac{\sin\theta}{2\cos\theta} \to \frac{dr}{r}=\frac{2\cos\theta}{\sin\theta}=2\cot\theta d\theta \)
- 양변을 적분하면 다음과 같다.
- \( \int \frac{dr}{r} = \int 2\cot\theta d\theta \)
- 좌변 적분 과정은 다음과 같다.
- \( \int \frac{dr}{r} = \ln{r} \)
- 우변 적분 과정은 다음과 같다.
- \( \int 2\cot\theta d\theta = 2\int \frac{\cos\theta}{\sin\theta}d\theta \)
- \( \sin\theta = u \to \cos\theta d\theta = du \)
- \( 2\int \frac{\cos\theta}{\sin\theta}d\theta = 2\int \frac{du}{u} = 2\ln{|u|} + C = 2\ln{|\sin\theta|} + C \)
- 적분한 양변을 정리하면 다음과 같다.
- \( \ln{r} = 2\ln{|\sin\theta|} + C = \ln{\sin^2\theta} + C \)
- \( r = e^C \sin^2\theta \)
- \( r = C \sin^2\theta \)
- 따라서 그림 2의 검정선(black line)과 같이 전계의 유선이 나타난다.
- \( C = 1, 1.5, 2, 2.5 \)
3) 쌍극자 모멘트(Dople Moment)
(1) 쌍극자 모멘트의 정의
- 반대 부호를 가진 두 전하 \( (+Q, -Q) \) 가 일정한 거리만큼 떨어져 있을 때 이 전하 쌍의 극성을 나타내는 벡터량
- 전하의 크기와 거리의 곱으로 정의된다.
- \( \mathbf{p} = Q\mathbf{d} (C\cdot m) \)
- 전기 쌍극자에 의한 전위식에 대입하면 다음과 같다.
- \( V = \frac{Qd}{4\pi\epsilon_0} \frac{\cos\theta}{r^2} \)
- \( \mathbf{d} \mathbf{a}_r = d\cos\theta \to Q\mathbf{d} = \mathbf{p} \mathbf{a}_r \)
- \( V = \frac{\mathbf{p}\mathbf{a}_r}{4\pi\epsilon_0 r^2} \)
- 거리에 대해 일반식으로 표현하면 다음과 같이 정리된다.
- \( \mathbf{r} = \mathbf{r}-\mathbf{r'} \)
- \( r \) : 전계 및 전위를 측정하는 점 P의 위치 벡터
- \( r' \) : 쌍극자의 중심을 결정하는 위치 벡터
- \( V = \frac{1}{4\pi\epsilon_0} \frac{ \mathbf{p}\cdot(\mathbf{r}- \mathbf{r'})}{|\mathbf{r}-\mathbf{r'}|^2} \)
(2) 쌍극자 모멘트의 특징
- 쌍극자 모멘트는 거리와 전하의 곱으로 결정되므로 다음과 같은 특징을 갖는다.
- p가 일정하다면 전하가 증가하고 거리가 감소해도 쌍극자 모멘트와 전위는 변하지 않는다.
- 쌍극자의 극한은 점 쌍극자로 정의된다
- 거리가 0에 수렴하고 Q가 무한대로 증가해도 그의 곱인 p가 유한하게 유지되는 경우이다.
- 유전체(Dielectric) 물질에 대해 다룰 때 다시 등장할 예정이다.
'Engineering Electromagnetism > 4. Electric Field Energy&Potential' 카테고리의 다른 글
| Chapter 4-6 정전계 내의 에너지 밀도(Energy Density in the Electrostatic Field) (0) | 2025.03.17 |
|---|---|
| Chapter 4-4 전위 경도(Potential Gradient) (0) | 2025.03.10 |
| Chapter 4-3 전하계에 의한 전위 : 보존적 성질 (0) | 2025.03.10 |
| Chapter 4-2 전위차와 전위의 정의 (0) | 2025.03.07 |
| Chapter 4-1 전계 내에서 점전하를 이동시키는데 소요되는 에너지 (0) | 2025.03.06 |



