Chapter 1-7 원통 좌표계(Circular Coordinate System)

 

 

1. 원통 좌표계 (Circular Coordinate System)

직각 좌표계에 이어 대칭성을 갖는 좌표계중 하나인 원통좌표계에 대해 알아보자.

 

 

1) 원통 좌표계의 정의

 

그림1. 극 좌표계(좌)와 원통 좌표계(우)

 

그림2. 원통 좌표계에 대한 세 평면

 

정의 : 점의 위치를 원점(기준점)으로부터의 거리, 회전각, 높이로 공간상의 한 점을 원통면 위의 점으로 표현하는 좌표계

 

극 좌표계 : \( (\rho , \phi) \)

평면상 한 기준점을 원점으로 정의

\( \rho \) : 원점으로부터 한 점까지의 거리

\( \phi \) : 그 점으로부터 원점에 이르는 직선과 기준 축 사이각 

 

원통 좌표계 : \( (\rho , \phi, z) \)

2차원 극좌표계의 표면에 수직 방향으로 z축을 정의하여 공간상의 한점을 원통면 위의 점으로 표시

\( \rho\) : 원통의 반지름

\( \phi \) : 원주각

\( z\) : 높이

z축 방향 : \( \phi \) 회전 방향에 오른손 법칙 적용

 

 

2) 원통 좌표계의 단위 벡터

 

그림3. 원통 좌표계의 단위 벡터

 

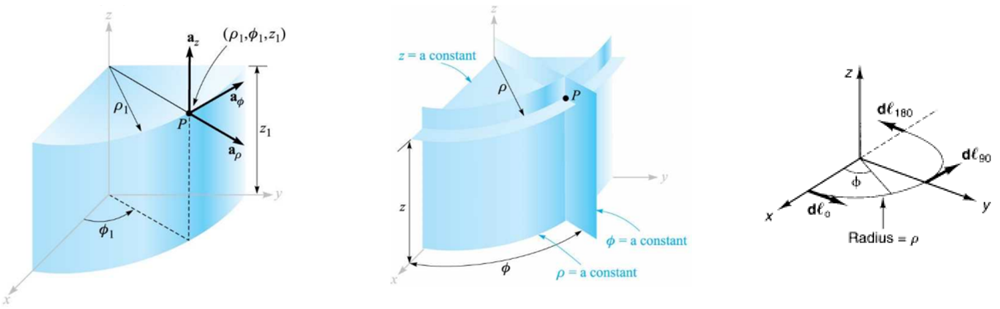
(1) 정의

좌표값이 일정한 면에 직각이고, 좌표값이 증가하는 방향의 크기가 1인 벡터

\( \mathbf{a_\rho} \) : 반지름 방향으로 원의 접선과 수직인 방향(원통면에 직각이고 원통 바깥쪽 방향)

\( \mathbf{a_\phi} \) : 원주 방향(원의 접선 방향)으로 반지름에 수직인 방향

\( \mathbf{a_z} \) : 직각 좌표계의 \(  \mathbf{a_z} \) 와 동일

 

(2) 특징

직각 좌표계에서는 각 축\( (x, y, z) \) 이 고정된 방향을 가지지만 원통 좌표계에서는 단위 벡터의 방향이 좌표(위치)에 따라 달라진다.
왜냐하면, 위치에 따라 개별 축의 값이 증가하는 방향이 다르기 때문에, 직각좌표계에서와 같이 일정한 방향성을 갖는 단위 벡터를 정의하는 것이 불가능하다.
따라서, 개별 위치(좌표)에 대하여 단위 벡터를 다음과 같이 정의한다.

 

점 \( (\rho_1 , \phi_1, z_1) \) 에서의 단위 벡터 : \( \mathbf{a_\rho} \) , \( \mathbf{a_\phi} \) , \( \mathbf{a_z} \)

 

단위 벡터는 서로 직교하므로 \( \mathbf{a_\rho} \times \mathbf{a_\phi} = \mathbf{a_z} \) 관계가 성립한다.

즉, 좌표계가 오른손 좌표계이다.

 

 

3) 원통 좌표계의 미소체적소 (Differential Volume Element)

 

그림4. 원통 좌표계의 미소체적소

 

한 점 \( (\rho , \phi, z) \) 에서 각 변수가 증가하는 방향으로 미소량 \( (d\rho , d\phi, dz) \) 을 증가시켜 6개면으로 둘러 쌓인 입체면 즉, 미소체적을 형성

 

입체면을 형성하는 미소체적소서의 길이, 면적, 체적은 다음과 같다.

• 길이(Length)
  • \( d\rho = d\rho \)
  • \( d\phi \) 의 경우, 호의 길이 공식 \( l=r\theta \) 에 의해 길이가 다음과 같이 정의된다.
  • \( d\phi = \rho d\phi \quad (\because r=\rho, \theta=\phi) \)
  • \( dz=dz \)
• 대각선 길이(Length)
  • \( dL = \sqrt{( d\rho )^2+( \rho d\phi )^2+(dz)^2} \)
• 면적(Surface)
  • \( dS = \rho d\rho \phi, \quad d\rho dz, \quad  \rho d\phi dz \)
• 체적(Volume)
  • \( dv = \rho d\rho \phi dz  \)

 

 

4) 원통좌표계와 직각좌표계의 관계

(1) 좌표 관계(위치 관계)

 

그림5. 원통 좌표계와 직각 좌표계의 변수 관계

 

좌표 관계는 한 점을 기준으로 직각좌표계 \( (x, y, z) \) 와 원통좌표계 \( (\rho, \phi, z) \) 변수간 관계를 의미한다.

점 P에서 각 축에 수선의 발을 내리면 직각이 형성되므로 사이각 \( \phi \) 와 삼각비를 이용하여 변수간 관계를 다음과 같이 정의할 수 있다.

 

\( x=\rho\cos\phi \quad \quad  \rho=\sqrt{x^2+y^2} \)

\(  y=\rho\sin\phi \quad \quad \phi=\arctan{y/x} \)

\( z=z \)

 

 

(2) 벡터 관계

 

그림6. 원통 좌표계와 직각 좌표계의 벡터 관계

 

벡터 관계는 각 단위 벡터를 기준으로 직각좌표계 \( \mathbf{a_x}, \mathbf{a_y} , \mathbf{a_z}  \) 와 원통좌표계 \(\mathbf{a_\rho}, \mathbf{a_\phi} , \mathbf{a_z} \) 벡터간 관계를 의미한다.

 

두 좌표계에 대한 두 벡터 \( \mathbf{A} \) 를 원통 좌표계에 대한 단위 벡터로 전개하면 다음과 같다.

$$ \mathbf{A} = A_x \mathbf{a_x} + A_y \mathbf{a_y} + A_z \mathbf{a_z}, \quad \mathbf{A} = A_{\rho} \mathbf{a_{\rho}} + A_{\phi} \mathbf{a_{\phi}} + A_z \mathbf{a_z} $$ $$ \begin{aligned} A_\rho &= \mathbf{A} \cdot \mathbf{a_\rho} = \left( A_x \mathbf{a_x} + A_y \mathbf{a_y} + A_z \mathbf{a_z} \right) \cdot \mathbf{a_\rho} \\ &= A_x \mathbf{a_x} \cdot \mathbf{a_\rho} + A_y \mathbf{a_y} \cdot \mathbf{a_\rho} + A_z \mathbf{a_z} \cdot \mathbf{a_\rho} \\ A_\phi &= \mathbf{A} \cdot \mathbf{a_\phi} = \left( A_x \mathbf{a_x} + A_y \mathbf{a_y} + A_z \mathbf{a_z} \right) \cdot \mathbf{a_\phi} \\ &= A_x \mathbf{a_x} \cdot \mathbf{a_\phi} + A_y \mathbf{a_y} \cdot \mathbf{a_\phi} + A_z \mathbf{a_z} \cdot \mathbf{a_\phi} \\ A_z &= \mathbf{A} \cdot \mathbf{a_z} = \left( A_x \mathbf{a_x} + A_y \mathbf{a_y} + A_z \mathbf{a_z} \right) \cdot \mathbf{a_z} \\ &= A_x \mathbf{a_x} \cdot \mathbf{a_z} + A_y \mathbf{a_y} \cdot \mathbf{a_z} + A_z \mathbf{a_z} \cdot \mathbf{a_z} \\ \end{aligned} $$

 

수식을 완성하기 위해 원통 좌표계와 직각 좌표계의 단위 벡터간 내적 관계가 필요하고 다음과 같다.

내적 관계는 그림6과 같이 사이각 \( \phi \) 와 삼각비를 이용하여 다음과 같이 정의할 수 있다.

$$ \begin{aligned} \mathbf{a_x} \cdot \mathbf{a_\rho} &= \cos\phi \\ \mathbf{a_x} \cdot \mathbf{a_\phi} &= -\sin\phi \\ \mathbf{a_x} \cdot \mathbf{a_z} &= 0 \end{aligned} \quad \begin{aligned} \mathbf{a_y} \cdot \mathbf{a_\rho} &= \sin\phi \\ \mathbf{a_y} \cdot \mathbf{a_\phi} &= \cos\phi \\ \mathbf{a_y} \cdot \mathbf{a_z} &= 0 \end{aligned} \quad \begin{aligned} \mathbf{a_z} \cdot \mathbf{a_\rho} &= 0 \\ \mathbf{a_z} \cdot \mathbf{a_\phi} &= 0 \\ \mathbf{a_z} \cdot \mathbf{a_z} &= 1 \end{aligned} $$

 

 

내적 관계를 이용하여 두 좌표계의 벡터 관계를 정의하면 다음과 같다.

$$ \begin{aligned} A_{\rho} &= \mathbf{A} \cdot \mathbf{a_{\rho}} = \left( A_x \mathbf{a_x} + A_y \mathbf{a_y} + A_z \mathbf{a_z} \right) \cdot \mathbf{a_{\rho}} \\ &= A_x \mathbf{a_x} \cdot \mathbf{a_{\rho}} + A_y \mathbf{a_y} \cdot \mathbf{a_{\rho}} \\ &= A_x \cos\phi + A_y \sin\phi \\[8pt] A_{\phi} &= \mathbf{A} \cdot \mathbf{a_{\phi}} = \left( A_x \mathbf{a_x} + A_y \mathbf{a_y} + A_z \mathbf{a_z} \right) \cdot \mathbf{a_{\phi}} \\ &= A_x \mathbf{a_x} \cdot \mathbf{a_{\phi}} + A_y \mathbf{a_y} \cdot \mathbf{a_{\phi}} \\ &= - A_x \sin\phi + A_y \cos\phi \\[8pt] A_{z} &= \mathbf{A} \cdot \mathbf{a_{z}} = \left( A_x \mathbf{a_x} + A_y \mathbf{a_y} + A_z \mathbf{a_z} \right) \cdot \mathbf{a_{z}} \\ &= A_z \end{aligned} $$ 따라서 정리하면 다음과 같다. $$ \begin{bmatrix} A_{\rho} \\ A_{\phi} \\ A_{z} \end{bmatrix} = \begin{bmatrix} \cos\phi & \sin\phi & 0 \\ -\sin\phi & \cos\phi & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} A_x \\ A_y \\ A_z \end{bmatrix} $$

 

(3) 정리

좌표(위치)의 변환과 벡터의 변환은 다르다.

좌표의 변환은 한 점을 변환하는 것이고,

벡터의 변환은 성분벡터와 단위벡터를 이용하여 해당 벡터 자체를 변환하는 것이다.